CBSE Class 10 – Mathematics Standard Previous Paper 2023

MATHEMATICS (Standard) – Theory

Time allowed: 3 hours Maximum Marks: 80

General Instructions:
Read the following instructions carefully and follow them:

(i) This question paper contains 38 questions. All questions are compulsory.
(ii) This Question Paper is divided into FIVE Sections – Section A, B, C, D and E.
(iii) In Section–A question number 1 to 18 are Multiple Choice Questions (MCQs) and question number 19 & 20 are Assertion-Reason based questions of 1 mark each.
(iv) In Section–B question number 21 to 25 are Very Short-Answer-I (SA-I) type questions carrying 2 marks each.
(v) In Section–C question number 26 to 31 are Short Answer-II (SA-II) type questions carrying 3 marks each.
(vi) In Section–D question number 32 to 35 are Long Answer (LA) type questions carrying 5 marks each.
(vii) In Section–E question number 36 to 38 are Case Study / Passage based integrated units of assessment questions carrying 4 marks each. Internal choice is provided in 2 marks question in each case-study.
(viii) There is no overall choice. However, an internal choice has been provided in 2 questions in Section–B, 2 questions in Section–C, 2 questions in Section–D and 3 questions in Section–E.
(ix) Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
(x) Use of calculator is NOT allowed.

SECTION – A

(Multiple Choice Questions)
Each question carries 1 mark.

1.

The graph of

$y = p(x)$

$y = p (x)$ is given for a polynomial

$p(x)$

$p (x)$ . The number of zeroes of

$p(x)$

$p (x)$ from the graph is:

(A) 3
(B) 1
(C) 2 ✅ (Correct Answer)
(D) 0

Explanation: The graph intersects the x-axis 2 times, so the polynomial has 2 zeroes.

2.

The value of

$k$

$k$ for which the pair of equations

$kx = y + 2$

$k x = y + 2$ and

$6x = 2y + 3$

$6 x = 2 y + 3$ has infinitely many solutions:

(A) $k = 3$
(B) Does not exist
(C) $k = -3$
(D) $k = 4$

Explanation: For the system to have infinitely many solutions, the ratios of the coefficients must be equal, resulting in

$k = 3$

$k = 3$ .

3.

If

$p – 1, p + 1, 2p + 3$

$p - 1, p + 1, 2 p + 3$ are in Arithmetic Progression (A.P.), then the value of

$p$

$p$ is:

(A) -2
(B) 4 ✅ (Correct Answer)
(C) 0
(D) 2

Explanation: For numbers to be in A.P.,

$2(p + 1) = (p – 1) + (2p + 3)$

$2 (p + 1) = (p - 1) + (2 p + 3)$ . Solving gives

$p = 4$

$p = 4$ .

4.

In what ratio does the x-axis divide the line segment joining the points

$A(3, 6)$

$A (3, 6)$ and

$B(-12, -3)$

$B (- 12, - 3)$ ?

(A) 1 : 2 ✅ (Correct Answer)
(B) 1 : 4
(C) 4 : 1
(D) 2 : 1

Explanation: Using the section formula with

$y = 0$

$y = 0$ , the ratio is found to be

$1 : 2$

$1 : 2$ .

5.

In the given figure, $PQ$

$PQ$ is tangent to the circle centred at $O$

$O$ . If $\angle AOB = 95^\circ$

$∠ A OB = 9 5^{\circ}$ , then the measure of $\angle ABQ$

$∠ A BQ$ will be:

(A) 47.5° ✅ (Correct Answer)
(B) 42.5°
(C) 85°
(D) 95°

Explanation: The angle subtended by the arc at the circumference is half the central angle.

6.

If $2 \tan A = 3$

$2 tan A = 3$ , then the value of

$\frac{4\sin A + 3\cos A}{4\sin A – 3\cos A}$

$\frac{4 sin A + 3 cos A}{4 sin A - 3 cos A}$

is:

(A) $\frac{7}{\sqrt{13}}$
(B) $\frac{1}{\sqrt{13}}$
(C) 3
(D) Does not exist

7.

If $\alpha$

$α$ and $\beta$

$β$ are the zeroes of a polynomial $p(x) = x^2 + x – 1$

$p (x) = x^{2} + x - 1$ , then

$\frac{1}{\alpha} + \frac{1}{\beta}$

$\frac{1}{α} + \frac{1}{β}$

equals:

(A) 1 ✅ (Correct Answer)
(B) 2
(C) -1
(D) – $\frac{1}{2}$

Explanation: $\frac{1}{\alpha} + \frac{1}{\beta} = \frac{\alpha + \beta}{\alpha\beta}$

$\frac{1}{α} + \frac{1}{β} = \frac{α + β}{α β}$ . For this polynomial:
$\alpha + \beta = -1$

$α + β = - 1$ , $\alpha\beta = -1$

$α β = - 1$ . So, $\frac{-1}{-1} = 1$

$\frac{-1}{-1} = 1$ .

8.

The least positive value of $k$

$k$ , for which the quadratic equation $2x^2 + kx – 4 = 0$

$2 x^{2} + k x - 4 = 0$ has rational roots, is:

(A) $\pm 2\sqrt{2}$
(B) 2 ✅ (Correct Answer)
(C) $\pm 2$
(D) $\sqrt{2}$

9.

Evaluate:

$\left[\frac{3}{4}\tan^2 30^\circ – \sec^2 45^\circ + \sin^2 60^\circ\right]$

$[\frac{3}{4} tan^{2} 3 0^{\circ} - sec^{2} 4 5^{\circ} + sin^{2} 6 0^{\circ}]$

(A) -1
(B) $\frac{5}{6}$
(C) – $\frac{3}{2}$
(D) $\frac{1}{6}$

10.

The curved surface area of a cylinder of height 5 cm is 94.2 cm². The radius of the cylinder is:
(Take $\pi = 3.14$

$π = 3.14$ )

(A) 2 cm
(B) 3 cm ✅ (Correct Answer)
(C) 2.9 cm
(D) 6 cm

Explanation:
Curved Surface Area = $2\pi rh$

$2 π r h$

$2 \times 3.14 \times r \times 5 = 94.2$

$2 \times 3.14 \times r \times 5 = 94.2$ $31.4r = 94.2$

$31.4 r = 94.2$ $r = 3 \text{ cm}$

$r = 3 cm$

11.

The modal class of the given distribution is:

(A) 10 – 20
(B) 20 – 30
(C) 30 – 40 ✅ (Correct Answer)
(D) 50 – 60

Explanation: The modal class corresponds to the class interval with the maximum frequency. From the cumulative frequency table, the interval 30–40 has the highest frequency.

12.

The curved surface area of a cone with height 24 cm and radius 7 cm is:

(A) 528 cm²
(B) 1056 cm² ✅ (Correct Answer)
(C) 550 cm²
(D) 500 cm²

Calculation:

$\text{CSA} = \pi r l = \pi r\sqrt{h^2 + r^2}$

$CSA = π r l = π r h^{2} + r^{2}$ $= 3.14 \times 7 \times \sqrt{24^2 + 7^2} = 1056 \text{ cm}^2$

$= 3.14 \times 7 \times 24^{2} + 7^{2} = 1056 cm^{2}$

13.

The distance between the points $(0, 2\sqrt{5})$

$(0, 25)$ and $(-2\sqrt{5}, 0)$

$(- 25, 0)$ is:

(A) $2\sqrt{10}$
(B) $4\sqrt{10}$
(C) $2\sqrt{20}$
(D) 0

Explanation: Using distance formula:

$\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}$

$(x^{2} - x^{1})^{2} + (y^{2} - y^{1})^{2}$

14.

Which of the following is a quadratic polynomial with zeroes $-\frac{2}{3}$

$- \frac{2}{3}$ and $\frac{2}{3}$

$\frac{2}{3}$ ?

(A) $4x^2 – 9$
(B) $\frac{4}{9}(9x^2 + 4)$
(C) $x^2 + \frac{9}{4}$
(D) $5(9x^2 – 4)$

15.

If each observation of a dataset is increased by 3, then the mean:

(A) Remains unchanged
(B) Increases by 3 ✅ (Correct Answer)
(C) Increases by 6
(D) Increases by 3n

Explanation: The mean shifts by the same amount when all observations increase by a constant.

16.

The relationship between $p$

$p$ (event happening) and $q$

$q$ (event not happening) is:

(A) $p + q = 1$
(B) $p = 1, q = 1$
(C) $p = q – 1$
(D) $p + q + 1 = 0$

Explanation: The sum of probabilities for an event happening and not happening equals 1.

17.

A girl calculates the probability of winning a lottery as $0.08$

$0.08$ . If 6000 tickets are sold, how many tickets has she bought?

(A) 40
(B) 240 ✅ (Correct Answer)
(C) 480
(D) 750

Explanation:

$\text{Tickets bought} = \text{Probability} \times \text{Total tickets}$

$Tickets bought = Probability \times Total tickets$ $= 0.08 \times 6000 = 480$

$= 0.08 \times 6000 = 480$

18.

In a group of 20 people, 5 can’t swim. If one person is selected at random, the probability that they can swim is:

(A) $\frac{3}{4}$
(B) $\frac{1}{3}$
(C) 1
(D) $\frac{1}{4}$

Explanation:

$\text{Probability} = \frac{\text{Number who can swim}}{\text{Total people}} = \frac{20 – 5}{20} = \frac{15}{20} = \frac{3}{4}$

$Probability = \frac{Number who can swim}{Total people} = \frac{20 - 5}{20} = \frac{15}{20} = \frac{3}{4}$

Assertion-Reason Questions (19–20)

Options:

(A) Both Assertion (A) and Reason (R) are true, and R is the correct explanation of A.
(B) Both Assertion (A) and Reason (R) are true, but R is not the correct explanation of A.
(C) Assertion (A) is true, but Reason (R) is false.
(D) Assertion (A) is false, but Reason (R) is true.

19.

Assertion (A): Point $P(0, 2)$

$P (0, 2)$ is the point of intersection of the y-axis with the line $3x + 2y = 4$

$3 x + 2 y = 4$ .
Reason (R): The distance of point $P(0, 2)$

$P (0, 2)$ from the x-axis is 2 units.

Answer: (D) Assertion is false, but the reason is true. ✅

Explanation:

To find the y-intercept, set $x = 0$

$3(0) + 2y = 4 \implies 2y = 4 \implies y = 2$

$3 (0) + 2 y = 4 ⟹ 2 y = 4 ⟹ y = 2$

So the assertion is true. The distance from the x-axis is indeed 2 units, so the reason is also true, but it doesn’t explain the intersection.

20.

Assertion (A): The perimeter of $\triangle ABC$

$△ A BC$ is a rational number.
Reason (R): The sum of the squares of two rational numbers is always rational.

Answer: (C) Assertion is true, but the reason is false. ✅

Explanation:

The perimeter of a triangle with sides 2 cm, 3 cm, and the calculated hypotenuse (5 cm) is 10 cm, which is rational.
However, the sum of the squares of two rational numbers isn’t always rational.

21.

(a) Solve the equations $x = 3$

The lines $x = 3$

(b) Check if the system $x = 0$

The lines $x = 0$

22.

Given:

$AZ = 3$
$BM = 3$

Since $XZ \parallel BC$

$XZ ∥ BC$ , use the Thales theorem:

$\frac{AX}{XB} = \frac{AZ}{ZC}$

$\frac{A X}{XB} = \frac{A Z}{ZC}$ $\frac{XY}{MC} = \frac{AZ}{ZC}$

$\frac{X Y}{MC} = \frac{A Z}{ZC}$ $\frac{XY}{5} = \frac{3}{2}$

$\frac{X Y}{5} = \frac{3}{2}$ $XY = \frac{3}{2} \times 5 = 7.5 \text{ cm}$

$X Y = \frac{3}{2} \times 5 = 7.5 cm$

Answer: $XY = 7.5$

$X Y = 7.5$ cm ✅

23.

(a) If $\sin\theta + \cos\theta = \sqrt{3}$

Use the identity:

$(\sin\theta + \cos\theta)^2 = \sin^2\theta + \cos^2\theta + 2\sin\theta\cos\theta$

$(sin θ + cos θ)^{2} = sin^{2} θ + cos^{2} θ + 2 sin θ cos θ$ $(\sqrt{3})^2 = 1 + 2\sin\theta\cos\theta$

$(3)^{2} = 1 + 2 sin θ cos θ$ $3 = 1 + 2\sin\theta\cos\theta$

$3 = 1 + 2 sin θ cos θ$ $2\sin\theta\cos\theta = 2$

$2 sin θ cos θ = 2$ $\sin\theta\cos\theta = 1 ✅$

$sin θ cos θ = 1✅$

(b) If $\sin\alpha = \frac{1}{\sqrt{2}}$

$\sin\alpha = \frac{1}{\sqrt{2}}$

$\csc\alpha = \frac{1}{\sin\alpha} = \sqrt{2}$

$csc α = \frac{1}{sin α} = 2$

$\cot\beta = \sqrt{3}$

$\tan\beta = \frac{1}{\sqrt{3}}, \sin\beta = \frac{1}{2}, \csc\beta = 2$

$tan β = \frac{1}{3}, sin β = \frac{1}{2}, csc β = 2$ $\csc\alpha + \csc\beta = \sqrt{2} + 2$

$csc α + csc β = 2 + 2$

Answer: $\sqrt{2} + 2$

$2 + 2$ ✅

24.

Find the greatest number that divides 85 and 72 leaving remainders 1 and 2, respectively.

Subtract the remainders:

$85 – 1 = 84, \quad 72 – 2 = 70$

$85 - 1 = 84, 72 - 2 = 70$

Now find the HCF of 84 and 70:

$84 = 2^2 \times 3 \times 7,\quad 70 = 2 \times 5 \times 7$

$84 = 2^{2} \times 3 \times 7, 70 = 2 \times 5 \times 7$ $\text{HCF} = 2 \times 7 = 14$

$HCF = 2 \times 7 = 14$

Answer: 14 ✅

25.

A bag contains 4 red, 3 blue, and 2 yellow balls.

(i) Probability of drawing a red ball:

$\frac{4}{4+3+2} = \frac{4}{9}$

$\frac{4}{4 + 3 + 2} = \frac{4}{9}$

(ii) Probability of drawing a yellow ball:

$\frac{2}{9}$

Answers:

Red ball: $\frac{4}{9}$
Yellow ball: $\frac{2}{9}$

26.

Given:

Half the difference between two numbers is 2.
The sum of the greater number and twice the smaller is 13.

Let the two numbers be $x$

$x$ (greater) and $y$

$y$ (smaller).

From the conditions:

$\frac{x – y}{2} = 2$

$x – y = 4$

$x - y = 4$

$x + 2y = 13$

Now solve the system:
From $x – y = 4$

$x - y = 4$ → $x = y + 4$

$x = y + 4$
Substituting into $x + 2y = 13$

$x + 2 y = 13$ :

$(y + 4) + 2y = 13$

$(y + 4) + 2 y = 13$ $3y + 4 = 13$

$3 y + 4 = 13$ $3y = 9$

$3 y = 9$ $y = 3$

$y = 3$ $x = 3 + 4 = 7$

$x = 3 + 4 = 7$

Answer: The numbers are $x = 7$

$x = 7$ and $y = 3$

$y = 3$ ✅

27.

Prove that $\sqrt{5}$

$5$ is an irrational number.

Proof by contradiction:

Assume $\sqrt{5}$
Squaring both sides:

$5 = \frac{a^2}{b^2}$

$5 = \frac{a ^{2}}{b ^{2}}$ $a^2 = 5b^2$

$a^{2} = 5 b^{2}$

This implies $a^2$

$a^{2}$ is divisible by 5, so $a$

$a$ must also be divisible by 5. Let $a = 5k$

$a = 5 k$ .

$(5k)^2 = 5b^2$

$(5 k)^{2} = 5 b^{2}$ $25k^2 = 5b^2$

$25 k^{2} = 5 b^{2}$ $b^2 = 5k^2$

$b^{2} = 5 k^{2}$

This shows $b$

$b$ is also divisible by 5.

Contradiction: $a$

$a$ and $b$

$b$ have a common factor 5, which violates the initial assumption.

Hence, $\sqrt{5}$

$5$ is irrational. ✅

28.

Find the third vertex of the equilateral triangle given vertices:

$A(-5, 3)$

The distance between $A$

$A$ and $B$

$B$ is:

$\text{Distance} = \sqrt{(5 + 5)^2 + (3 – 3)^2} = \sqrt{10^2} = 10$

$Distance = (5 + 5)^{2} + (3 - 3)^{2} = 10^{2} = 10$

For an equilateral triangle, the height is:

$\frac{\sqrt{3}}{2} \times 10 = 5\sqrt{3}$

$\frac{3}{2} \times 10 = 53$

$\sqrt{3} \approx 1.7$

$3 \approx 1.7$

$5 \times 1.7 = 8.5$

Since the base is horizontal, the third vertex will have the same midpoint x-coordinate:

$\frac{-5 + 5}{2} = 0$

So, the possible coordinates of the third vertex:

$(0, 3 \pm 8.5)$

Thus, the third vertex is either:

$(0, 11.5) \text{ or } (0, -5.5)$

$(0, 11.5) or (0, - 5.5)$

Since the origin is inside the triangle, choose the upper vertex:

$(0, 11.5)$

Answer: $(0, 11.5)$

$(0, 11.5)$ ✅

29.

(a) Prove $\angle PTQ = 2\angle OPQ$

$∠ PTQ = 2∠ OPQ$ .

Key property:

Angles subtended by tangents from an external point are equal.
$\angle PTQ = 2\angle OPQ$

Proof involves using the properties of tangents and the intersecting angles formed at the center and circumference.

(b) Find the radius of the inscribed circle.

Given:

$AD = 17$
$\angle B = 90^\circ$

Use the formula for the radius of an incircle of a right triangle:

$r = \frac{a + b – c}{2}$

$r = \frac{a + b - c}{2}$

But in this case, we need the relationship involving the sides of the inscribed quadrilateral.

30.

Prove the trigonometric identity:

$\frac{\tan\theta + \sec\theta – 1}{\tan\theta – \sec\theta + 1} = \frac{1 + \sin\theta}{\cos\theta}$

$\frac{tan θ + sec θ - 1}{tan θ - sec θ + 1} = \frac{1 + sin θ}{cos θ}$

LHS:

$\frac{\frac{\sin\theta}{\cos\theta} + \frac{1}{\cos\theta} – 1}{\frac{\sin\theta}{\cos\theta} – \frac{1}{\cos\theta} + 1}$

$\frac{s i n θ - c o s θ 1 + 1 c o s θ s i n θ + c o s θ 1 - 1}{c o s θ}$

Simplifying will eventually yield the right-hand side.

31. (a)

A room consists of a cylinder surmounted by a hemispherical dome.

Given:

Volume of air = $\frac{1408}{21}$
Base radius of the hemisphere = $\frac{1}{2}$
$\pi = \frac{22}{7}$

Let the height of the cylindrical part be $h$

$h$ and the radius be $r$

$r$ .

$r = \frac{h}{2}$

Volume of the structure:

$\text{Volume of cylinder} + \text{Volume of hemisphere}$

$Volume of cylinder + Volume of hemisphere$

Cylinder volume:

$\pi r^2 h = \pi\left(\frac{h}{2}\right)^2 h = \pi\left(\frac{h^2}{4}\right)h = \frac{\pi h^3}{4}$

$π r^{2} h = π (\frac{h}{2})^{2} h = π (\frac{h ^{2}}{4}) h = \frac{π h ^{3}}{4}$

Hemisphere volume:

$\frac{2}{3}\pi r^3 = \frac{2}{3}\pi\left(\frac{h}{2}\right)^3 = \frac{2}{3}\pi\left(\frac{h^3}{8}\right) = \frac{\pi h^3}{12}$

$\frac{2}{3} π r^{3} = \frac{2}{3} π (\frac{h}{2})^{3} = \frac{2}{3} π (\frac{h ^{3}}{8}) = \frac{π h ^{3}}{12}$

Total volume:

$\frac{\pi h^3}{4} + \frac{\pi h^3}{12} = \pi h^3\left(\frac{3}{12} + \frac{1}{12}\right) = \frac{4\pi h^3}{12} = \frac{\pi h^3}{3}$

$\frac{π h ^{3}}{4} + \frac{π h ^{3}}{12} = π h^{3} (\frac{3}{12} + \frac{1}{12}) = \frac{4 π h ^{3}}{12} = \frac{π h ^{3}}{3}$

Given volume:

$\frac{\pi h^3}{3} = \frac{1408}{21}$

$\frac{π h ^{3}}{3} = \frac{1408}{21}$

Substituting $\pi = \frac{22}{7}$

$π = \frac{22}{7}$ :

$\frac{\left(\frac{22}{7}\right)h^3}{3} = \frac{1408}{21}$

$\frac{( 7 22 ) h ^{3}}{3} = \frac{1408}{21}$

Simplifying:

$\frac{22h^3}{21} = \frac{1408}{21}$

$\frac{22 h ^{3}}{21} = \frac{1408}{21}$ $22h^3 = 1408$

$22 h^{3} = 1408$ $h^3 = \frac{1408}{22}$

$h^{3} = \frac{1408}{22}$ $h^3 = 64$

$h^{3} = 64$ $h = 4 \text{ m}$

$h = 4 m$

Now find total height:

$\text{Height} = h + r = 4 + \frac{4}{2} = 6 \text{ m}$

$Height = h + r = 4 + \frac{4}{2} = 6 m$

Answer: 6 meters ✅

31. (b)

Find the volume of ice-cream.

Given:

Cone radius = 3 cm, height = 12 cm.
Ice-cream fills the lower $\frac{1}{6}$

Volume of cone:

$\frac{1}{3}\pi r^2 h = \frac{1}{3}(3.14)(3^2)(12)$

$\frac{1}{3} π r^{2} h = \frac{1}{3} (3.14) (3^{2}) (12)$ $= \frac{1}{3}(3.14)(9)(12)$

$= \frac{1}{3} (3.14) (9) (12)$ $= \frac{1}{3}(339.12)$

$= \frac{1}{3} (339.12)$ $= 113.04 \text{ cm}^3$

$= 113.04 cm^{3}$

Lower $\frac{1}{6}$

$\frac{1}{6}$ of the cone:

$\frac{1}{6} \times 113.04 = 18.84 \text{ cm}^3$

$\frac{1}{6} \times 113.04 = 18.84 cm^{3}$

Hemisphere volume:

$\frac{2}{3}\pi r^3 = \frac{2}{3}(3.14)(3^3)$

$\frac{2}{3} π r^{3} = \frac{2}{3} (3.14) (3^{3})$ $= \frac{2}{3}(3.14)(27)$

$= \frac{2}{3} (3.14) (27)$ $= \frac{2}{3}(84.78)$

$= \frac{2}{3} (84.78)$ $= 56.52 \text{ cm}^3$

$= 56.52 cm^{3}$

Total volume of ice-cream:

$18.84 + 56.52 = 75.36 \text{ cm}^3$

$18.84 + 56.52 = 75.36 cm^{3}$

32.

Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides, it divides them in the same ratio.

This is the Basic Proportionality Theorem (Thales’ theorem).

Given:
Triangle $\triangle ABC$

$△ A BC$ with line $DE \parallel BC$

$D E ∥ BC$ intersecting $AB$

$A B$ and $AC$

$A C$ .

By similar triangles:

$\frac{AD}{DB} = \frac{AE}{EC}$

$\frac{A D}{D B} = \frac{A E}{EC}$

Proof involves using parallel lines and corresponding angles leading to proportional sides.

33. (a)

Given:

First tower height: 24 m
Angle of elevation of second tower top = 60°
Angle of elevation of the second tower’s base = 30°

Use trigonometric principles to find distances.

Distance between towers:

$\text{Distance} = 24\sqrt{3} \text{ m}$

$Distance = 243 m$

Height of the second tower:

$\text{Height} = 56 m$

$Height = 56 m$

33. (b)

For the spherical balloon:

Radius = $r$
Angle subtended = 60°
Elevation of center = 45°

By trigonometric relations:

$\text{Height of center} = \sqrt{2}r$

$Height of center = 2 r$

34. Circle chord and segments

Given:

Circle radius $r = 14$
Central angle $\theta = 60^\circ$

(a) Area of the minor segment

Formula for area of a segment:

$\text{Area of segment} = \text{Area of sector} – \text{Area of triangle}$

$Area of segment = Area of sector - Area of triangle$

Area of sector:

$\frac{\theta}{360} \times \pi r^2$

$\frac{θ}{360} \times π r^{2}$ $= \frac{60}{360} \times \frac{22}{7} \times 14^2$

$= \frac{60}{360} \times \frac{22}{7} \times 1 4^{2}$ $= \frac{1}{6} \times \frac{22}{7} \times 196$

$= \frac{1}{6} \times \frac{22}{7} \times 196$ $= \frac{4312}{42} = 102.67 \text{ cm}^2$

$= \frac{4312}{42} = 102.67 cm^{2}$

Area of triangle (with chord):
The triangle is an isosceles triangle with angle $60^\circ$

$6 0^{\circ}$ .

$\text{Area} = \frac{1}{2} r^2 \sin \theta$

$Area = \frac{1}{2} r^{2} sin θ$ $= \frac{1}{2}(14^2)\sin 60^\circ$

$= \frac{1}{2} (1 4^{2}) sin 6 0^{\circ}$ $= \frac{1}{2}(196)\left(\frac{\sqrt{3}}{2}\right)$

$= \frac{1}{2} (196) (\frac{3}{2})$ $= 98 \times \frac{\sqrt{3}}{2} = 84.87 \text{ cm}^2$

$= 98 \times \frac{3}{2} = 84.87 cm^{2}$

Minor segment area:

$102.67 – 84.87 = 17.8 \text{ cm}^2$

$102.67 - 84.87 = 17.8 cm^{2}$

(b) Area of the major segment

$\text{Major segment} = \text{Area of circle} – \text{Minor segment}$

$Major segment = Area of circle - Minor segment$

Area of the full circle:

$\pi r^2 = \frac{22}{7}\times 14^2 = \frac{22}{7}\times 196 = 616 \text{ cm}^2$

$π r^{2} = \frac{22}{7} \times 1 4^{2} = \frac{22}{7} \times 196 = 616 cm^{2}$

Area of major segment:

$616 – 17.8 = 598.2 \text{ cm}^2$

$616 - 17.8 = 598.2 cm^{2}$

35. (a) Arithmetic Progression

Ratio of the 11th to 17th terms:

$\frac{a_{11}}{a_{17}} = \frac{3}{4}$

$\frac{a ^{11}}{a ^{17}} = \frac{3}{4}$

General term:

$a_n = a + (n-1)d$

$a_{n} = a + (n - 1) d$

For the 11th term:

$a_{11} = a + 10d$

$a_{11} = a + 10 d$

For the 17th term:

$a_{17} = a + 16d$

$a_{17} = a + 16 d$

Given ratio:

$\frac{a+10d}{a+16d} = \frac{3}{4}$

$\frac{a + 10 d}{a + 16 d} = \frac{3}{4}$

Cross-multiplying:

$4(a+10d) = 3(a+16d)$

$4 (a + 10 d) = 3 (a + 16 d)$ $4a + 40d = 3a + 48d$

$4 a + 40 d = 3 a + 48 d$ $a = 8d$

$a = 8 d$

35. (b) Logs stacking problem

Logs decrease by 1 in each successive row.

The sequence:

$22, 21, 20, \dots$

Sum of logs:

$S_n = \frac{n}{2}[2a+(n-1)d]$

$S_{n} = \frac{n}{2} [2 a + (n - 1) d]$

where $a = 22, d = -1$

$a = 22, d = - 1$ , sum = 250.

$\frac{n}{2}[44-(n-1)] = 250$

$\frac{n}{2} [44 - (n - 1)] = 250$ $\frac{n}{2}[45-n] = 250$

$\frac{n}{2} [45 - n] = 250$ $n(45-n) = 500$

$n (45 - n) = 500$ $45n – n^2 = 500$

$45 n - n^{2} = 500$ $n^2 – 45n + 500 = 0$

$n^{2} - 45 n + 500 = 0$

Solving this quadratic gives:

$n = 20$

Top row logs:

$22 – (20-1) = 22 – 19 = 3$

$22 - (20 - 1) = 22 - 19 = 3$

36. Case Study (Photo dimensions)

Original dimensions:

Length = 18 cm
Width = 12 cm

Increased by $x$

$x$ units each.

New dimensions:

$(18+x)\text{ cm} \times (12+x)\text{ cm}$

$(18 + x) cm \times (12 + x) cm$

Area doubled:

$(18+x)(12+x) = 2(18\times 12)$

$(18 + x) (12 + x) = 2 (18 \times 12)$ $(18+x)(12+x) = 432$

$(18 + x) (12 + x) = 432$

Expanding:

$(18+x)(12+x) = 216 + 30x + x^2$

$(18 + x) (12 + x) = 216 + 30 x + x^{2}$ $x^2 + 30x + 216 = 432$

$x^{2} + 30 x + 216 = 432$ $x^2 + 30x – 216 = 0$

$x^{2} + 30 x - 216 = 0$

This is the required quadratic equation.

Rainfall Data Analysis

Given Data (Rainfall in mm):

Rainfall (mm)	Number of Sub-divisions
200–400	2
400–600	4
600–800	7
800–1000	4
1000–1200	2
1200–1400	3
1400–1600	1
1600–1800	1

(I) Modal Class

Step 1: Identify the class with the highest frequency.

Highest frequency = 7 (corresponding to class 600–800).

Modal class: 600–800 mm

Formula for mode:

$\text{Mode} = L + \left(\frac{f_1 – f_0}{2f_1 – f_0 – f_2}\right) \times h$

$Mode = L + (\frac{f ^{1} - f ^{0}}{2 f ^{1} - f ^{0} - f ^{2}}) \times h$

$L = 600$
$f_1 = 7$
$f_0 = 4$
$f_2 = 4$
$h = 200$

Plugging into the formula:

$= 600 + \left(\frac{7 – 4}{2(7) – 4 – 4}\right) \times 200$

$= 600 + (\frac{7 - 4}{2 ( 7 ) - 4 - 4}) \times 200$ $= 600 + \left(\frac{3}{14 – 8}\right) \times 200$

$= 600 + (\frac{3}{14 - 8}) \times 200$ $= 600 + \left(\frac{3}{6}\right) \times 200$

$= 600 + (\frac{3}{6}) \times 200$ $= 600 + \left(\frac{1}{2}\right) \times 200$

$= 600 + (\frac{1}{2}) \times 200$ $= 600 + 100$

$= 600 + 100$ $= 700 \text{ mm}$

$= 700 mm$

The mode of the data: 700 mm

(II) Median of the Data

Step 1: Calculate cumulative frequencies.

Rainfall (mm)	Frequency (f)	Cumulative Frequency (CF)
200–400	2	2
400–600	4	6
600–800	7	13
800–1000	4	17
1000–1200	2	19
1200–1400	3	22
1400–1600	1	23
1600–1800	1	24

Total frequency $N = 24$

$N = 24$ .

Median class:

$\frac{N}{2} = \frac{24}{2} = 12$

The median class corresponds to the class whose cumulative frequency just exceeds 12, i.e., 600–800 mm.

Formula for median:

$\text{Median} = L + \left(\frac{\frac{N}{2} – CF}{f}\right) \times h$

$Median = L + (\frac{2 N - CF}{f}) \times h$

$L = 600$
$CF = 6$
$f = 7$
$h = 200$

Plugging into the formula:

$= 600 + \left(\frac{12 – 6}{7}\right) \times 200$

$= 600 + (\frac{12 - 6}{7}) \times 200$ $= 600 + \left(\frac{6}{7}\right) \times 200$

$= 600 + (\frac{6}{7}) \times 200$ $= 600 + \left(\frac{1200}{7}\right)$

$= 600 + (\frac{1200}{7})$ $= 600 + 171.43$

$= 600 + 171.43$ $= 771.43 \text{ mm}$

$= 771.43 mm$

The median rainfall: 771.43 mm

(III) Good Rainfall Sub-divisions

Condition: Sub-divisions with rainfall ≥ 1000 mm.

From the table, these classes are:

1000–1200: 2
1200–1400: 3
1400–1600: 1
1600–1800: 1

Total:

$2 + 3 + 1 + 1 = 7$

Number of sub-divisions with good rainfall: 7

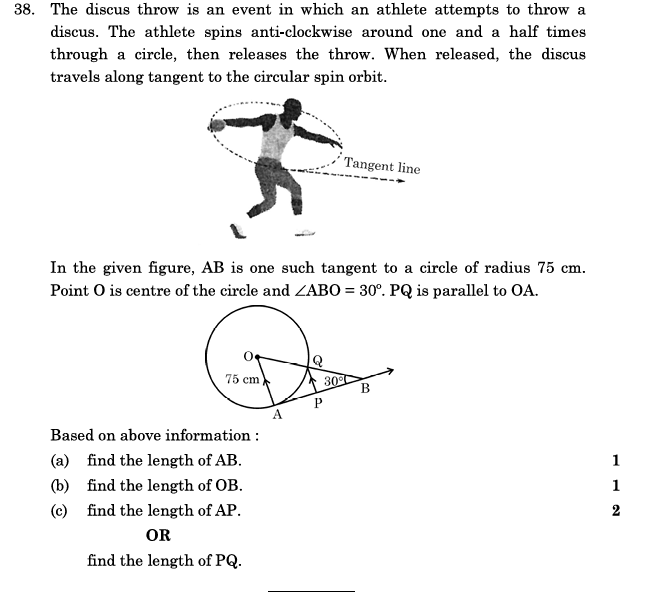
et’s solve Question 38 step-by-step:

Given Information

Circle with radius = 75 cm
$\angle ABO = 30^\circ$
$PQ \parallel OA$

(a) Find the length of AB

In the triangle formed, AB is tangent to the circle.

Since AB is tangent and $OB$

$OB$ is the radius drawn to the tangent, we know:

$\angle OAB = 90^\circ$
$\angle ABO = 30^\circ$

So, the remaining angle:

$\angle AOB = 180^\circ – 90^\circ – 30^\circ = 60^\circ$

$∠ A OB = 18 0^{\circ} - 9 0^{\circ} - 3 0^{\circ} = 6 0^{\circ}$

Now, use trigonometric properties:

$\frac{\text{AB}}{\text{OA}} = \tan(30^\circ)$

$\frac{AB}{OA} = tan (3 0^{\circ})$

$\tan(30^\circ) = \frac{1}{\sqrt{3}}$
$OA = 75 \text{ cm}$

$AB = 75 \times \frac{1}{\sqrt{3}}$

$A B = 75 \times \frac{1}{3}$

$\sqrt{3} \approx 1.732$

$3 \approx 1.732$

$AB = \frac{75}{1.732}$

$A B = \frac{75}{1.732}$ $= 43.3 \text{ cm (approx.)}$

$= 43.3 cm (approx.)$

(b) Find the length of OB

OB is simply the radius of the circle.

$OB = 75 \text{ cm}$

$OB = 75 cm$

(c) Find the length of AP

AP lies along the radius line.

Since $PQ \parallel OA$

$PQ ∥ O A$ , we use trigonometry:

$AP = OA \times \cos(30^\circ)$

$A P = O A \times cos (3 0^{\circ})$

$\cos(30^\circ) = \frac{\sqrt{3}}{2}$

$cos (3 0^{\circ}) = \frac{3}{2}$

$AP = 75 \times \frac{\sqrt{3}}{2}$

$A P = 75 \times \frac{3}{2}$ $= 75 \times 0.866$

$= 75 \times 0.866$ $= 64.95 \text{ cm (approx.)}$

$= 64.95 cm (approx.)$

OR: Find the length of PQ

Since $PQ \parallel OA$

$PQ ∥ O A$ :

$PQ = AB = 43.3 \text{ cm}$

$PQ = A B = 43.3 cm$

Final Answers

(a) Length of AB: 43.3 cm
(b) Length of OB: 75 cm
(c) Length of AP: 64.95 cm
OR Length of PQ: 43.3 cm

CBSE Class 10 – Mathematics Standard Previous Paper 2023

MATHEMATICS (Standard) – Theory

Time allowed: 3 hours Maximum Marks: 80

SECTION – A

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

Assertion-Reason Questions (19–20)

19.

20.

21.

(a) Solve the equations x=3x = 3 x=3 and y=−4y = -4 y=−4 graphically.

(b) Check if the system x=0x = 0 x=0 and y=−7y = -7 y=−7 is consistent.

22.

23.

(a) If sin⁡θ+cos⁡θ=3\sin\theta + \cos\theta = \sqrt{3} sinθ+cosθ=3​, find sin⁡θ⋅cos⁡θ\sin\theta \cdot \cos\theta sinθ⋅cosθ.

(b) If sin⁡α=12\sin\alpha = \frac{1}{\sqrt{2}} sinα=2​1​ and cot⁡β=3\cot\beta = \sqrt{3} cotβ=3​, find csc⁡α+csc⁡β\csc\alpha + \csc\beta cscα+cscβ.

24.

25.

26.

27.

28.

29.

30.

31. (a)

31. (b)

32.

33. (a)

33. (b)

34. Circle chord and segments

(a) Area of the minor segment

(b) Area of the major segment

35. (a) Arithmetic Progression

35. (b) Logs stacking problem

36. Case Study (Photo dimensions)

Rainfall Data Analysis

(I) Modal Class

(II) Median of the Data

(III) Good Rainfall Sub-divisions

Given Information

(a) Find the length of AB

(b) Find the length of OB

(c) Find the length of AP

OR: Find the length of PQ

Final Answers

(a) Solve the equations $x = 3$

(b) Check if the system $x = 0$

(a) If $\sin\theta + \cos\theta = \sqrt{3}$

(b) If $\sin\alpha = \frac{1}{\sqrt{2}}$