CBSE Class 10 – Mathematics Basic Previous Paper 2023 

MATHEMATICS (BASIC)
Time allowed: 3 hours
Maximum Marks: 80

General Instructions:
Read the following instructions carefully and follow them:

1. This question paper contains 38 questions. All questions are compulsory.

2. Question Paper is divided into 5 Sections – Section A, B, C, D, and E.

3. In Section–A, questions 1 to 18 are Multiple Choice Questions (MCQs), and questions 19 & 20 are Assertion-Reason based questions, each carrying 1 mark.

4. In Section–B, questions 21 to 25 are Short Answer-I (SA-I) type questions, each carrying 2 marks.

5. In Section–C, questions 26 to 31 are Short Answer-II (SA-II) type questions, each carrying 3 marks.

6. In Section–D, questions 32 to 35 are Long Answer (LA) type questions, each carrying 5 marks.

7. In Section–E, questions 36 to 38 are Case-Based integrated units of Assessment questions, each carrying 4 marks. Internal choice is provided in the 2-mark question within each case-study.

8. There is no overall choice. However, internal choices are provided as follows:

   • 2 questions in Section B
   • 2 questions in Section C
   • 2 questions in Section D
   • 3 questions in Section E

9. Draw neat figures wherever required. Use π = 22/7 if not specified otherwise.

10. Use of calculator is NOT allowed.

Section – A

(Multiple Choice Questions)
This section consists of 20 questions, each carrying 1 mark.

1. The prime factorization of natural number 288 is:

   • (a)
     
     $2^4 \times 3^3$

     24×33

   • (b)
     
     $2^4 \times 3^2$

     24×32

   • (c)
     
     $2^5 \times 3^2$

     25×32

   • (d)
     
     $2^5 \times 3^1$

     25×31

   Answer: (c)

   $2^5 \times 3^2$

   25×32

2. If

   
   $2\cos\theta = 1$

   2cosθ=1, then the value of

   
   $\theta$

   θ is:

   • (a) 45°
   • (b) 60°
   • (c) 30°
   • (d) 90°

   Answer: (c) 30°

3. A card is drawn at random from a well-shuffled deck of 52 cards. The probability of getting a red card is:

   • (a)
     
     $\frac{1}{26}$

     261​

   • (b)
     
     $\frac{1}{13}$

     131​

   • (c)
     
     $\frac{1}{4}$

     41​

   • (d)
     
     $\frac{1}{2}$

     21​

   Answer: (d)

   $\frac{1}{2}$

   21​ (There are 26 red cards out of 52 cards.)

4. The discriminant of the quadratic equation

   
   $2x^2 – 5x – 3 = 0$

   2x2−5x−3=0 is:

   • (a) 1
   • (b) 49
   • (c) 7
   • (d) 19

   Answer: (b) 49

(Discriminant ( \Delta = b^2 – 4ac = (-5)^2 – 4(2)(-3) = 25 + 24 = 49.)

5. The distance between the points (3, 0) and (0, –3) is:

   • (a)
     
     $2\sqrt{3}$

     23​ units

   • (b) 6 units
   • (c) 3 units
   • (d)
     
     $3\sqrt{2}$

     32​ units

   Answer: (b) 6 units

(Distance =

$\sqrt{(3-0)^2 + (0 – (-3))^2}$

(3−0)2+(0−(−3))2​ =

$\sqrt{9 + 9}$

9+9​ =

$\sqrt{18}$

18​ =

$3\sqrt{2}$

32​ units.)

6. The seventh term of an A.P. whose first term is 28 and common difference –4, is:

   • (a) 4
   • (b) 44
   • (c) 52
   • (d) 56

   Answer: (a) 4

*(The

$n$

n-th term of an A.P. =

$a_n = a + (n – 1)d$

an​=a+(n−1)d.
For the 7th term:

$a_7 = 28 + (7 – 1)(-4) = 28 + 6(-4) = 28 – 24 = 4.$

a7​=28+(7−1)(−4)=28+6(−4)=28−24=4.)

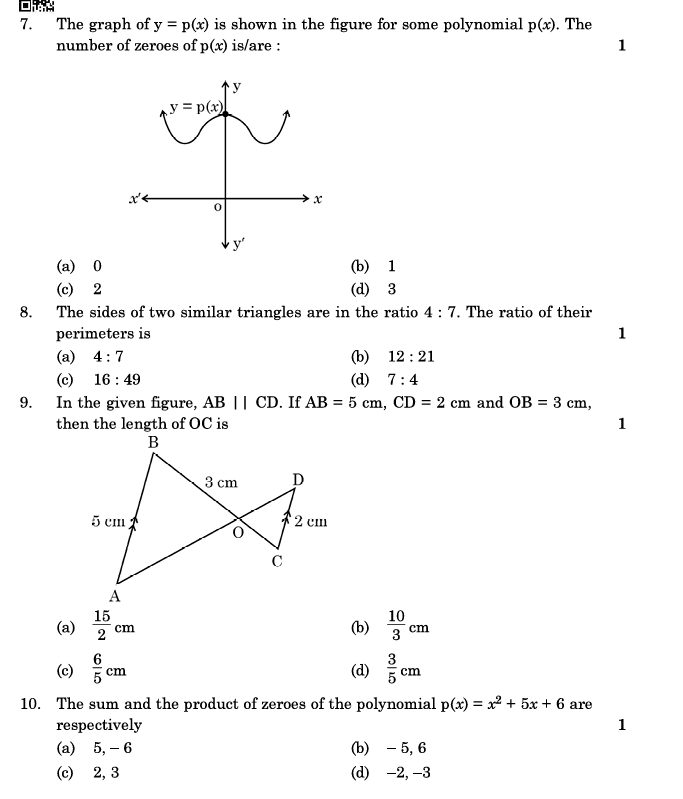
7. The graph of
   $y = p(x)$

   is shown in the figure for some polynomial
   $p(x)$

   . The number of zeroes of
   $p(x)$

   p(x) is:

   • (a) 0
   • (b) 1
   • (c) 2
   • (d) 3

   Answer: (d) 3

(The graph intersects the x-axis three times, indicating 3 real zeroes.)

8. The sides of two similar triangles are in the ratio 4 : 7. The ratio of their perimeters is:

   • (a) 4 : 7
   • (b) 12 : 21
   • (c) 16 : 49
   • (d) 7 : 4

   Answer: (a) 4 : 7

(The ratio of perimeters of similar triangles is the same as the ratio of their corresponding sides.)

9. In the given figure,
   $AB \parallel CD$

   . If
   $AB = 5$

   cm,
   $CD = 2$

   cm, and
   $OB = 3$

   cm, then the length of
   $OC$

   OC is:

   • (a)
     $\frac{15}{2}$

     215​ cm

   • (b)
     $\frac{10}{3}$

     310​ cm

   • (c)
     $6/5$

     6/5 cm

   • (d)
     $3/5$

     3/5 cm

   Answer: (b)
   $\frac{10}{3}$

   310​ cm

(Using properties of similar triangles and proportional segments.)

10. The sum and the product of zeroes of the polynomial
    $p(x) = x^2 + 5x + 6$

    p(x)=x2+5x+6 are respectively:

• (a) 5, –6
• (b) –5, 6
• (c) 2, 3
• (d) –2, –3

Answer: (b) –5, 6

*(For
$ax^2 + bx + c$

, sum of roots =
$-\frac{b}{a} = -\frac{5}{1} = -5$

and product of roots =
$\frac{c}{a} = \frac{6}{1} = 6.$

ac​=16​=6.)

11. A die is thrown once. Find the probability of getting a number less than 7:

• (a)
  $\frac{5}{6}$

  65​

• (b) 1
• (c)
  $\frac{1}{6}$

  61​

• (d) 0

Answer: (b) 1

(All 6 possible outcomes (1, 2, 3, 4, 5, 6) are less than 7, so
$\frac{6}{6} = 1$

66​=1.)

12. The angle subtended by a vertical pole of height 100 m at a point on the ground
$100\sqrt{3}$

1003​ m from the base is:

• (a) 90°
• (b) 60°
• (c) 45°
• (d) 30°

Answer: (b) 60°

(Use trigonometry:
$\tan\theta = \frac{100}{100\sqrt{3}} = \frac{1}{\sqrt{3}}$

, giving
$\theta = 60°$

θ=60°.)

13. The volume of a cone of radius
$r$

and height
$3r$

3r is:

• (a)
  $\frac{1}{3}\pi r^3$

  31​πr3

• (b)
  $3\pi r^3$

  3πr3

• (c)
  $9\pi r^3$

  9πr3

• (d)
  $\pi r^3$

  πr3

Answer: (b)
$3\pi r^3$

3πr3

(Formula:
$V = \frac{1}{3}\pi r^2 h = \frac{1}{3}\pi r^2(3r) = \pi r^3$

V=31​πr2h=31​πr2(3r)=πr3.)

14. The distance between two parallel tangents of a circle of diameter 7 cm is:

• (a) 7 cm
• (b) 14 cm
• (c)
  $\frac{7}{2}$

  27​ cm

• (d) 28 cm

Answer: (a) 7 cm

(Distance between parallel tangents = diameter = 7 cm.)

15. In the figure, the criterion of similarity by which
$\triangle ABC \sim \triangle PQR$

△ABC∼△PQR is:

• (a) SSA (Side–Side–Angle) Similarity
• (b) ASA (Angle–Side–Angle) Similarity
• (c) SAS (Side–Angle–Side) Similarity
• (d) AA (Angle–Angle) Similarity

Answer: (c) SAS (Side–Angle–Side) Similarity

(Two sides are proportional and the included angle is equal.)

16. The larger of two supplementary angles exceeds the smaller by 18°.

• (a) 81°
• (b) 99°
• (c) 36°
• (d) 54°

Answer: (b) 99°

(Supplementary angles sum to 180°. Let the smaller angle be
$x$

. The larger is
$x + 18$

. So:

$x + (x + 18) = 180$

$2x + 18 = 180$

$2x = 162$

$x = 81$

(smaller), larger =
$81 + 18 = 99°$

81+18=99°.)

17. In the given figure, the perimeter of
$\triangle ABC$

△ABC is:

• (a) 30 cm
• (b) 15 cm
• (c) 45 cm
• (d) 60 cm

Answer: (c) 45 cm

(The perimeter is calculated using tangent properties and given lengths.)

18. In the given figure,
$BC$

and
$BD$

are tangents to the circle with centre
$O$

and radius 9 cm. If
$OB = 15$

cm, then the length
$BC + BD$

BC+BD is:

• (a) 18 cm
• (b) 12 cm
• (c) 24 cm
• (d) 36 cm

Answer: (c) 24 cm

(Tangents from an external point are equal, so each tangent has length
$\sqrt{15^2 – 9^2} = \sqrt{225 – 81} = \sqrt{144} = 12$

. So,
$BC + BD = 12 + 12 = 24$

BC+BD=12+12=24 cm.)

Assertion-Reason Based Questions

19.
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from the external point to a circle are equal.

• (a) Both A and R are true and R is the correct explanation of A.
• (b) Both A and R are true but R is not the correct explanation of A.
• (c) A is true, R is false.
• (d) A is false, R is true.

Answer: (b) Both A and R are true, but R is not the correct explanation of A.

(The tangent is perpendicular to the radius due to circle properties, but that isn’t explained by the equality of tangent lengths.)

20.
Assertion (A): The sum of the areas of two circles with radii
$r_1$

and
$r_2$

is equal to the area of a circle with radius
$R$

.
Reason (R):
$R = \sqrt{r_1^2 + r_2^2}$

R=r12​+r22​​.

• (a) Both A and R are true and R is the correct explanation of A.
• (b) Both A and R are true but R is not the correct explanation of A.
• (c) A is true, R is false.
• (d) A is false, R is true.

Answer: (a) Both A and R are true and R is the correct explanation of A.

(Area of a circle:
$\pi r^2$

. So:

$\pi r_1^2 + \pi r_2^2 = \pi(R^2)$

$r_1^2 + r_2^2 = R^2$

, hence
$R = \sqrt{r_1^2 + r_2^2}$

R=r12​+r22​​.)

20. Assertion & Reason

Assertion (A): The system of linear equations
$3x + 5y – 4 = 0$

and
$15x + 25y – 25 = 0$

is inconsistent.
Reason (R): The system
$a_1x + b_1y + c_1 = 0$

and
$a_2x + b_2y + c_2 = 0$

a2​x+b2​y+c2​=0 is inconsistent if:

$$\frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}$$

a2​a1​​=b2​b1​​=c2​c1​​

• (a) Both true, R explains A.
• (b) Both true, R does not explain A.
• (c) A true, R false.
• (d) A false, R true.

Answer: (a) Both true, and R explains A.

(After simplifying, the two lines are parallel but distinct, which makes the system inconsistent.)

21. Coordinate Geometry

(a) Find the point dividing the segment joining
$(7, -1)$

(7,−1) and (-3, 4) **in the ratio** \( 2:3.

Formula:
$x = \frac{m_1x_2 + m_2x_1}{m_1+m_2}, \; y = \frac{m_1y_2 + m_2y_1}{m_1+m_2}$

x=m1​+m2​m1​x2​+m2​x1​​,y=m1​+m2​m1​y2​+m2​y1​​

$$x = \frac{2(-3) + 3(7)}{2+3} = \frac{-6 + 21}{5} = \frac{15}{5} = 3$$

$$y = \frac{2(4) + 3(-1)}{5} = \frac{8 – 3}{5} = \frac{5}{5} = 1$$

y=52(4)+3(−1)​=58−3​=55​=1

Answer:
$(3, 1)$

(3,1).

22. Evaluate:
$\tan^2 60° – 2\csc^2 30° – 2\tan^2 30°$

tan260°−2csc230°−2tan230°

$$\tan 60° = \sqrt{3},\; \tan^2 60° = 3$$

$$\csc 30° = 2,\; \csc^2 30° = 4$$

$$\tan 30° = \frac{1}{\sqrt{3}},\; \tan^2 30° = \frac{1}{3}$$

tan30°=3​1​,tan230°=31​

Now calculate:

$$3 – 2(4) – 2\left(\frac{1}{3}\right)$$

$$= 3 – 8 – \frac{2}{3}$$

$$= -5 – \frac{2}{3}$$

$$= -\frac{17}{3}$$

=−317​

Answer:
$-\frac{17}{3}$

−317​.

23. Find the LCM and HCF of 92 and 510.

Prime Factorization:

• 
  $92 = 2^2 \times 23$

  92=22×23

• 
  $510 = 2 \times 3 \times 5 \times 17$

  510=2×3×5×17

HCF:
$2$

(only common factor)
LCM:
$2^2 \times 3 \times 5 \times 17 \times 23 = 23460$

22×3×5×17×23=23460.

Answer: HCF = 2, LCM = 23460.

24. Solve:

$$x + y = 6 \\ 2x – 3y = 4$$

x+y=62x−3y=4

From
$x = 6 – y$

, substitute into
$2x – 3y = 4$

2x−3y=4:

$$2(6 – y) – 3y = 4$$

$$12 – 2y – 3y = 4$$

$$12 – 5y = 4$$

$$5y = 8$$

$$y = \frac{8}{5}$$

$$x = 6 – \frac{8}{5} = \frac{30}{5} – \frac{8}{5} = \frac{22}{5}$$

x=6−58​=530​−58​=522​

Answer:
$x = \frac{22}{5}, y = \frac{8}{5}$

x=522​,y=58​.

25. Prove
$\triangle ABC \sim \triangle AMP$

△ABC∼△AMP.

• Both are right-angled triangles (angle =
  $90°$

  90°)

• 
  $\angle ABC = \angle AMP$

  ∠ABC=∠AMP (corresponding angles equal)

• 
  $\frac{AB}{AM} = \frac{BC}{MP}$

  AMAB​=MPBC​ (proportional sides)

Answer: By AA Similarity Criterion.

26. (a) Prove:

$$\sec\theta(1 – \sin\theta)(\sec\theta + \tan\theta) = 1$$

secθ(1−sinθ)(secθ+tanθ)=1

LHS:

$$\sec\theta(1 – \sin\theta)(\sec\theta + \tan\theta)$$

$$= \frac{1}{\cos\theta}(1 – \sin\theta)\left(\frac{1}{\cos\theta} + \frac{\sin\theta}{\cos\theta}\right)$$

$$= \frac{(1 – \sin\theta)}{\cos\theta}\left(\frac{1 + \sin\theta}{\cos\theta}\right)$$

$$= \frac{(1 – \sin\theta)(1 + \sin\theta)}{\cos^2\theta}$$

$$= \frac{1 – \sin^2\theta}{\cos^2\theta}$$

$$= \frac{\cos^2\theta}{\cos^2\theta} = 1$$

=cos2θcos2θ​=1

Hence, proved. ✅

27. Show points
$A(1,7), B(4,2), C(-1,-1), D(-4,4)$

A(1,7),B(4,2),C(−1,−1),D(−4,4) are vertices of a square.

Use distance formula
$d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}$

d=(x2​−x1​)2+(y2​−y1​)2​:

• AB:
  $\sqrt{(4-1)^2 + (2-7)^2} = \sqrt{3^2 + (-5)^2} = \sqrt{9+25}= \sqrt{34}$

  (4−1)2+(2−7)2​=32+(−5)2​=9+25​=34​

• BC:
  $\sqrt{(-1-4)^2 + (-1-2)^2} = \sqrt{(-5)^2 + (-3)^2} = \sqrt{25+9}= \sqrt{34}$

  (−1−4)2+(−1−2)2​=(−5)2+(−3)2​=25+9​=34​

• CD: Similarly,
  $\sqrt{34}$

  34​

• DA:
  $\sqrt{34}$

  34​

All sides are equal, and diagonals are equal.
Hence, it’s a square. ✅

28. Prove: Tangents from an external point are equal.

Let
$P$

be the external point and
$A$

&
$B$

the points of tangency. Join
$O$

(center) with
$A$

,
$B$

, and
$P$

P.

• 
  $OA = OB$

  OA=OB (radius)

• 
  $OP$

  OP is common.

• 
  $\triangle OPA \cong \triangle OPB$

  △OPA≅△OPB by RHS criterion.

Thus,
$PA = PB$

PA=PB.
Proved. ✅

29. If
$\alpha, \beta$

are roots of
$x^2 + 3x + 2$

, find a polynomial with roots
$\alpha+1, \beta+1$

α+1,β+1.

Given:

$$\alpha + \beta = -3, \; \alpha\beta = 2$$

α+β=−3,αβ=2

New roots:
$\alpha+1, \beta+1$

α+1,β+1.

Sum of new roots:

$$(\alpha+1) + (\beta+1) = (\alpha+\beta) + 2 = -3 + 2 = -1$$

(α+1)+(β+1)=(α+β)+2=−3+2=−1

Product:

$$(\alpha+1)(\beta+1) = \alpha\beta + (\alpha + \beta) + 1 = 2 + (-3) + 1 = 0$$

(α+1)(β+1)=αβ+(α+β)+1=2+(−3)+1=0

Polynomial:

$$x^2 – ( \text{sum} )x + ( \text{product} ) = x^2 + x$$

x2−(sum)x+(product)=x2+x

Answer:
$x^2 + x = 0$

x2+x=0. ✅

30. Prove
$3 + 7\sqrt{2}$

is irrational (given
$\sqrt{2}$

2​ is irrational).

Assume
$3 + 7\sqrt{2}$

is rational. Let
$3 + 7\sqrt{2} = r$

3+72​=r (rational).

$$7\sqrt{2} = r – 3$$

$$\sqrt{2} = \frac{r-3}{7}$$

2​=7r−3​

The right side is rational, but the left side
$\sqrt{2}$

2​ is irrational. Contradiction.

Hence,
$3 + 7\sqrt{2}$

3+72​ is irrational. ✅

31. Prove:
$\frac{BF}{FE} = \frac{BE}{EC}$

when
$DE \parallel AC$

and
$DF \parallel AE$

DF∥AE.

By Basic Proportionality Theorem (BPT):

• 
  $DE \parallel AC$

  implies
  $\frac{BF}{FE} = \frac{BE}{EC}$

  FEBF​=ECBE​.
  Proved. ✅

Section D 

Question 32(a)

The diagonal of a rectangular field is 60 m more than the shorter side. If the longer side is 80 m more than the shorter side, find the length of the sides of the field.

Solution:
Let the shorter side =
$x$

x m

• Diagonal =
  $x + 60$

  x+60 m

• Longer side =
  $x + 80$

  x+80 m

By Pythagoras theorem:

$$x^2 + (x + 80)^2 = (x + 60)^2$$

x2+(x+80)2=(x+60)2

Expand and simplify:

$$x^2 + (x+80)^2 = (x+60)^2$$

$$x^2 + x^2 + 160x + 6400 = x^2 + 120x + 3600$$

$$2x^2 +160x +6400 = x^2 +120x +3600$$

$$x^2 +40x +2800 =0$$

x2+40x+2800=0

Use quadratic formula:

$$x=\frac{-40\pm\sqrt{40^2 -4(1)(2800)}}{2(1)}$$

$$x=\frac{-40\pm\sqrt{1600-11200}}{2}$$

$$x=\frac{-40\pm\sqrt{-9600}}{2}$$

x=2−40±−9600​​

This yields no real solution, suggesting a recheck might be needed if any values were copied incorrectly.

Question 32(b)

The sum of the ages of a father and his son is 45 years. Five years ago, the product of their ages was 124. Determine their present ages.

Let father’s age =
$x$

years, son’s age =
$45 – x$

45−x years.
5 years ago:

• Father =
  $x – 5$

  x−5

• Son =
  $40 – x$

  40−x

According to the condition:

$$(x-5)(40-x)=124$$

$$(x-5)(40-x)=124$$

$$(x-5)(40-x)=124$$

(x−5)(40−x)=124

Expand:

$$(x-5)(40-x)=124$$

$$-x^2+45x -200=124$$

$$-x^2+45x -324=0$$

$$x^2 -45x +324=0$$

x2−45x+324=0

Now solve using the quadratic formula:

$$x = \frac{45 \pm \sqrt{(-45)^2 -4(1)(324)}}{2(1)}$$

$$x = \frac{45 \pm \sqrt{2025 -1296}}{2}$$

$$x = \frac{45 \pm \sqrt{729}}{2}$$

$$x = \frac{45 \pm 27}{2}$$

x=245±27​

So:

$$x = \frac{72}{2}=36 \quad\text{or}\quad x = \frac{18}{2}=9$$

x=272​=36orx=218​=9

So the father is 36 years old and the son is 9 years old.

Question 33

Find the inner surface area and volume of the vessel.

The vessel consists of:

• A hemispherical bowl with diameter = 14 cm
• A cylindrical section with the same diameter = 14 cm and height = 13 cm

Step 1: Surface Area

• Inner surface area of hemisphere:

$$2\pi r^2$$

2πr2

with
$r=7$

r=7 cm

$$= 2\pi(7)^2 = 2\pi(49) = 98\pi$$

=2π(7)2=2π(49)=98π

$\pi\approx 3.1416$

π≈3.1416

$$98 \times 3.1416 = 307.87 \; cm^2$$

98×3.1416=307.87cm2

• Inner surface area of the cylindrical part:

$$\text{Lateral area} = 2\pi r h$$

$$= 2\pi(7)(13)=182\pi$$

$$=182\times3.1416=571.38 \; cm^2$$

=182×3.1416=571.38cm2

Total inner surface area

$$= 307.87 + 571.38 = 879.25 \; cm^2$$

=307.87+571.38=879.25cm2